Binary Tree
Note: The following explanation is based on a recent proposal from Binary Trees. The design is expected to change as more people from the community provide feedback.
Overview
Using Binary Trees for the state tree is not a new idea. Back in 2020, this idea was explored in EIP-3102. Then, SNARKs were still in the early stages, and soon after, Verkle Trees became a more promising approach, so this direction was abandoned.
Many years have passed, and around mid-2024, two main motivations started to reignite the possibility of reconsidering Binary Trees compared to Verkle Trees.
The first one was some breakthroughs in quantum computers, which raised the concern that they could be a potential risk in 10 or 15 years. There’s no consensus around interpreting recent events, so there’s still the possibility that they will take many more years or never be a real risk for elliptic curve cryptography. Depending on how conservative core developers want to be, this might be a significant decision factor. Also note that if Verkle Trees are deployed, at least one extra state tree conversion is guaranteed to happen.
The second one is the rapid pace of improvement of SNARK/STARK proving systems. The speed at which they can provide proving throughput for hashes has been improving rapidly without requiring absurd hardware specs. Depending on the hash function used, the proving performance is or isn’t enough for L1 needs — we’ll dive more into this later.
In summary, a Binary Tree construction is now again a potential option for a SNARK-friendly state tree with other tradeoffs compared with the Verkle Tree.
Tree design
The currently proposed EIP-7864 pulls many ideas from EIP-6800, which are still helpful. These include many of the desired properties described in the Data Encoding page.
The tree construction is more straightforward than Verkle Trees since it relies only on a hash function for merkelization. The arity of the tree is defined as two since this arity minimizes the proof sizes. To learn more details, refer to the corresponding rationale section of the EIP.
Given a tree key, we define the first 31-bytes as the stem. This stem defines the main path where the 256 values are determined by the last byte of the tree key. This is better described by the diagram presented in the EIP:
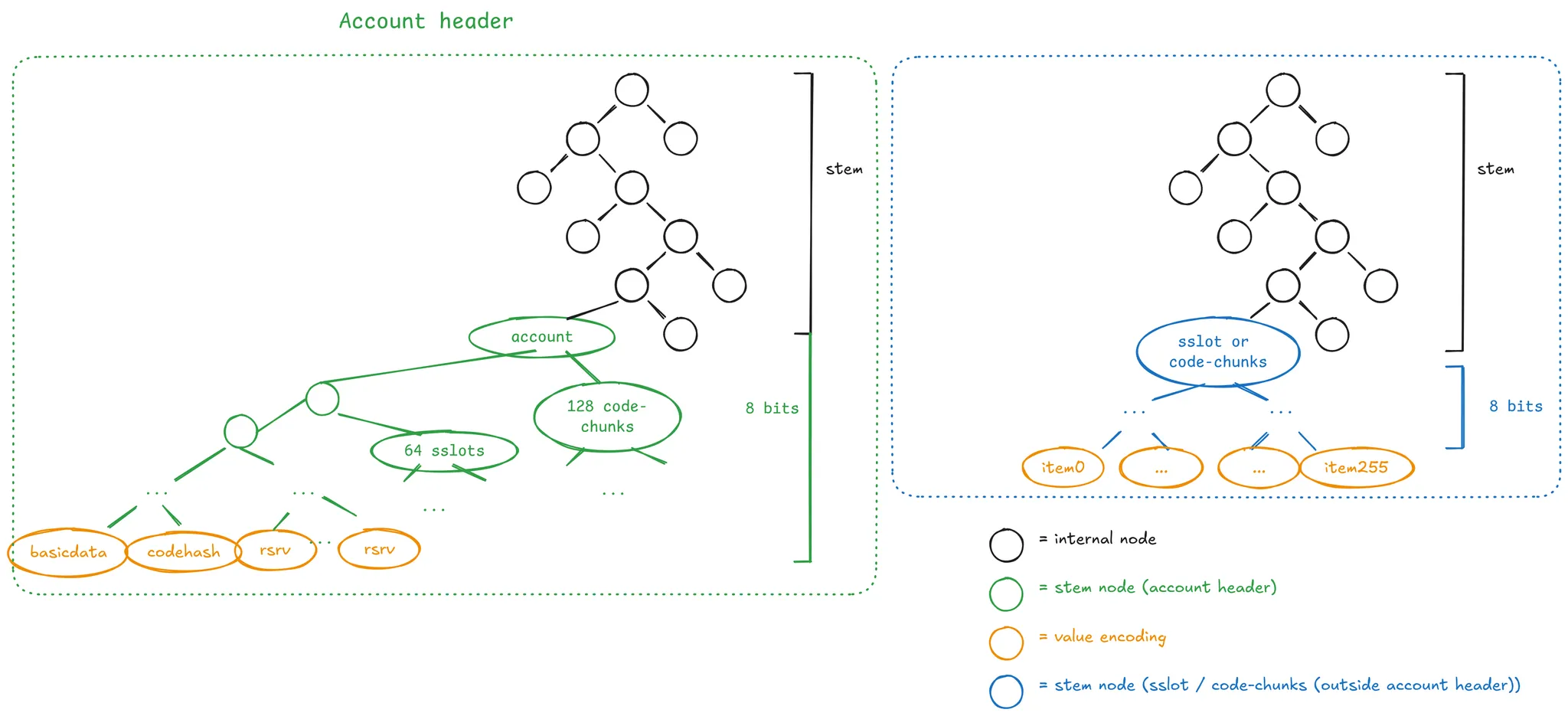
Given a tree key value to be inserted:
- With the first 31-bytes, we walk the black nodes (i.e., internal nodes). Starting with the most significant bit, each bit walks the tree downstream from the root.
- When we reach an internal node representing an empty subtree, we insert the leaf-level subtree, a full Merkle tree with 256 leaves. Said differently, the 256 values for this stem are a full tree with 8 levels.
- Depending on the last byte of the tree key, we store the desired value in the corresponding leaf.
This idea is the same as Verkle Trees, where each stem stores 256 values corresponding to the last byte of the tree key. Instead of using vector commitments, we use a full Merkle tree as a form of vector commitment.
The tree is merkelized using a hash function which allows us to hash 32-bytes -> 32-bytes and (32-bytes, 32-bytes) -> 32-bytes. Any secure hash function can be used with this construction. The current EIP proposed Blake3 as a conservative one, but this isn’t fully decided—more about it in the next section.
Proof Construction
If we need to build a Binary Tree proof for a list of key values, we have two options:
- Build a usual Merkle Tree. This is not different from how you can build proofs in the current Merkle Patricia Tree. The construction will be much more straightforward, i.e., we don’t have accounts and storage tries but a unified state tree, no RLP is used for encoding nodes data, etc. Also, the arity of the tree generates smaller proofs.
- For an L1 block required pre-state, a worst-case scenario still generates a tree proof that is bigger than desired. For these cases, we can create a SNARK/STARK proof, which is a Merkle Proof verifier in a proven circuit. This requires more work to generate, but the proof is smaller.
Hash function for merkelization
When using SNARKS/STARKs to generate a state-proof check, the proving performance is heavily influenced by the hash function used for merkelization. Normal cryptographic hash functions such as Keccak and Blake3 aren’t designed to be efficiently proven in circuits. Other cryptographic hash functions, such as Posiedon2 (i.e., arithmetic hash functions), are specifically designed to be efficiently proven in SNARKs. Their main difference is that arithmetic hash functions don’t rely on bitwise operations but directly work on desired finite fields matching the underlying proving system.
The current proving performance on desired hardware specs for normal hash functions such as Keccak or Blake3 is still an order of magnitude slower than required for L1 blocks. Hence, we must wait for them to keep improving in performance or for them to need more powerful hardware for block builders.
However, if we have an arithmetic hash function such as Poseidon2, the current proving performance on target hardware is more than enough for L1 block needs. The main drawback is that Poseidon2 is still not considered safe for use in L1. The Ethereum Foundation cryptography team has recently launched a public initiative to assess its security more formally. From another perspective, multiple zk-L2 have been using Poseidon for some years, which indirectly means billions of dollars publicly at stake — while this isn’t a formal bug bounty program, any black hat hacker that knows how to break the hash function could already attack these networks. This doesn’t prove Poseidon is safe, but it gives an optimistic perspective while the formal assessment is done.
Ideally, the Binary Tree should use Poseidon2 since it offers the best-proving performance. This allows block builders to have lower hardware specs, which is good for decentralization. Moreover, it’s crucial that proving the hash function doesn’t get in the way of bumping the block gas limit to keep improving L1 scaling. Hopefully, protocol developers can make a final call on this front within the next year.